斎藤研・杉本研合同基礎輪講 2015

第3回：射影変換・座標系変換・エピポーラ幾何(3月9日~3月13日)

3週目は，射影変換・座標系変換・エピポーラ幾何を扱います．
とくに，AR(Augmented Reality)などの技術では，3次元情報と2次元情報を変換する座標系変換が非常に重要です．
今週のトピックに関連して３つの行列について学びます．「H-Matrix」, 「P-Matrix」，「F-Matrix」の3つです．
イメージモザイキングでは「H-Matrix」，カメラキャリブレーションでは「P-Matrix」，エピポーラ幾何では「F-Matrix」を学習します．

1.イメージモザイキング

2つの画像の視点の対応を取ることで，パノラマ画像を生成することが可能です．
その際，重要となる技術が，射影変換というものです．
射影変換を行うことで疑似的に別視点からの画像を生成することができます.
射影変換する際に，必要な情報として，H-Matrixがあります．

H-Matrixについて

ある視点の画像を別の視点に射影変換する行列がH-Matrixです．
H-Matrixは，２つの画像中の対応点を取ることで，求める事が可能です．
以下に入力画像を示します．


視点1	視点2

これらの画像に対して，対応点を取ることで，H-Matrixを計算することができます．
下に対応点を取った各視点画像，視点１の画像を視点2に変換した結果画像を表示します．

対応点・視点変換結果

視点変換後，２枚の画像を重ね合わせる事でパノラマ画像を作成することができます．

余談ですが，ちゃんと対応点を取ったのに変換が上手くいかなかった人はいますか？
対応点を正しく４点以上とれていたとしても，変換が上手くいかないときもあります．(ヒント：対応する点の３次元的な奥行き…。)
基礎輪講やこれからの研究でもそうですが，うまくいった結果だけ見せるのではなく，
うまくいかなかった結果を見せ，その考察や改善を発表するという事も大事です．失敗は恥ずべきことではありません．そのようなスタンスで今後も取り組んで言ってください．

2.カメラキャリブレーション

ここでは，主に座標系について学びます．主に座標系は4つあります．

・画像座標系

・正規化画像座標系

・カメラ座標系

・世界座標系

各座標系がどういうものなのか，緑本などから勉強しましょう．
また，各座標系は行列を用いる事で変換することが可能です．(例:カメラ座標系 ⇒ 世界座標系)
変換する行列はどのようなパラメータが必要なのか，どういう原理で変換することができるのかを理解しましょう．

P-Matrixについて

P-Matrixは画像座標系から世界座標系に変換する行列になります．ARの技術では非常に重要な行列なので理解しておきましょう．
以下に，P-Matrixを用いて座標系の変換例を示します．
P-MatrixはA,R,tの各行列の積を取った行列になります(詳しくは緑本で…．)
A行列は，カメラの内部パラメータによる行列．R,t行列はカメラの外部パラメータによる行列になります.
下左図に示すマーカに対して，各行列成分は以下のようになります．
A行列はカメラ固有の値を持った行列になり，R,t行列は画像中の世界座標を定める事で求める事が可能になります．
P-Matrixを用いると，下右図のようにマーカに対して立方体を描画することが可能です．


マーカ画像	立方体描画画像

世界座標系について

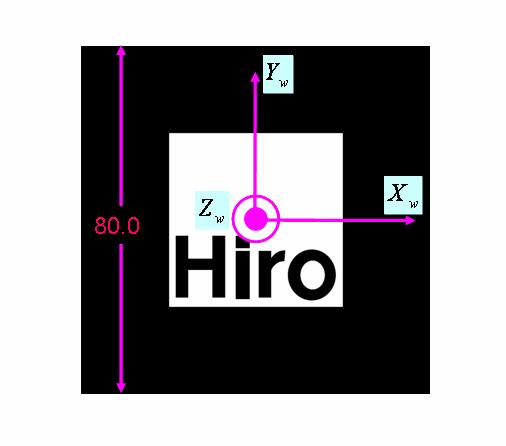
世界座標系は図の様にマーカ中心を原点とした座標系とし，
X軸・Y軸はマーカ平面上に，Z軸はマーカ平面に垂直で裏から表に向かうものとします．
描画する立方体は世界座標系で一辺の長さが80.0とし，マーカを覆い隠す様に描画して下さい．
立方体の8頂点の座標は以下のようになります．
(-40.0,-40.0,0.0),(-40.0,40.0,0.0),(40.0,40.0,0.0),(40.0,-40.0,0.0),(-40.0,-40.0,0.80.0),(-40.0,40.0,80.0),(40.0,40.0,80.0),(40.0,-40.0,80.0)
これらの頂点を結ぶように直線を描画することで立方体を描画することができます．
描画関数についてはOpenCVにあるので，調べておきましょう．

世界座標系とマーカの関係

3.エピポーラ幾何（空間位置の計算，エピポーラ線）

2つの画像間の幾何学的関係を表すのにエピポーラ幾何というものがあります．
これは視点１から見ている視線が，視点2からどういう風に見えているかを算出することができます．
その際に重要となる行列がF-Matrixです．
F-Matrixが何をする式なのか，どのように導かれた式なのか理解しておきましょう．
また，ここは専門用語も多い部分なので，しっかり勉強しておきましょう．

F-Matrixについて

F-Matrixは２つの視点画像において，対応点を取ることで求める事が出来ます．
以下に，F-Matrixを算出し，エピポーラ線を描画する例を示します．
入力は，異なる２つの視点の画像を用います．


視点1	視点2

これらの画像に対して，対応点を取ることで，F-Matrixを算出します．
エピポーラ線描画のために，画像中の投影点を選択しておきます．
以下に各対応点，投影点の選択した様子，エピポーラ線を描画した結果を示します．

作業2

対応点・エピポーラ線描画結果

描画されたエピポーラ線は，視点2の画像において，視点1の投影点を通る視線を描画しています．
実装の際に，様々な実験，考察を行うと良いです．例えば…
・最低限必要な対応点の数は？
・対応点をとってもうまくいかない例は？うまくいく例は？
・エピポーラ幾何を応用した例は？
このようなことを実験したり，調べたりすることで，発表の内容の質が向上するかと思います．